Différences entre versions de « P2E-DIE »
(→Code) |
|||
| (57 versions intermédiaires par le même utilisateur non affichées) | |||
| Ligne 2 : | Ligne 2 : | ||
== Dé binaire == | == Dé binaire == | ||
| − | + | L'idée dans ce projet est de choisir un nombre au hasard entre 1 et 6 lorsque l'utilisateur presse sur un bouton (pour lancer le dé). | |
| − | + | Depuis la plus tendre enfance, nous sommes tous habitué à utiliser la base 10. Ainsi, la lecture d'une valeur numérique quelconque n'est généralement pas un problème... et encore moins pour un dé offrant une valeur entre 1 et 6 en chiffre ou dé utilisant 1 à 6 points. | |
| − | Par | + | Malheureusement, le Pico-2-Explorer ne dispose pas de LEDs organisées sous la forme de dé ou afficheur numérique. Par contre la carte dispose de 3 LEDs qui peuvent être utilisée pour afficher des 1 (allumée) et des 0 (éteinte). |
| + | |||
| + | [[Fichier:P2E-DIE-intro-00.jpg|360px]] | ||
| + | |||
| + | Il est possible d'utiliser les LEDs du Pico-2-explorer pour représenter une valeur numérique à l'aide d'un encodage binaire. | ||
| + | |||
| + | Nous pourrons ainsi produire une valeur numérique de 1 à 6 (celles d'un dé) qu'il sera possible de lire sur les 3 LEDs du Pico-2-Explorer. | ||
| + | |||
| + | La connaissance des premières représentations binaire peut s'avérer très utile dans les mondes de l'informatique et de l'électronique. | ||
| + | |||
| + | == A propos de l'encodage binaire == | ||
| + | |||
| + | Plutôt que d'aborder l'encodage binaire de front, je vais procéder par une approche détournée suivit d'une petite correction. | ||
| + | |||
| + | === Une approche imparfaite === | ||
| + | |||
| + | Admettons que l'on fixe une valeur prédéterminée à nos trois LEDs. Soit les valeurs 1, 2, 3 (en commençant la numérotation par la gauche). | ||
| + | |||
| + | [[Fichier:P2E-DIE-intro-10.jpg|360px]] | ||
| + | |||
| + | Il est donc possible d'indiquer les valeurs suivantes en allumant la LED appropriée. On peu indiquer quelle LED est allumée à l'aide d'une suite de 1 et de 0. Par exemple 001 indique que seule la LED la plus a droite est allumée tandis que 110 indique que les deux LEDs les plus a gauches sont allumées. | ||
| + | |||
| + | Chacun de ces 1/0 sont des équivalents de marche/arret ou vrai/faux ou True/False. Chacune des positions, appelée bit, n'a que deux valeurs possibles. | ||
| + | |||
| + | * 000 = Aucune LED = 0 | ||
| + | * 001 = LED verte = 1 | ||
| + | * 010 = LED orange = 2 | ||
| + | * 100 = LED rouge = 3 | ||
| + | |||
| + | En allant un peu plus loin et en sommant les valeurs correspondantes, il est même possible d'atteindre la valeur 6. | ||
| + | |||
| + | Ainsi: | ||
| + | * 101 = LED rouge + LED verte = 3 + 1 = 4 | ||
| + | * 110 = LED rouge + LED orange = 3 + 2 = 5 | ||
| + | * 111 = LED rouge + LED orange + LED verte = 3 + 2 + 1 = 6 | ||
| + | |||
| + | {{dbox-gray| Avec cette approche, nous pouvons déjà déterminer de cette petite démonstration que: | ||
| + | # Le bit le plus à droite à le poids le plus faible (une valeur de 1). | ||
| + | # Le bit le plus a gauche à le poids le plus fort (une valeur de 3). | ||
| + | Nous pouvons aussi donner des noms aux différents bits: | ||
| + | # Le bit de poids le plus faible (le plus à droite) porte le nom de bit 0 (ou b0), | ||
| + | # Le bit suivant, directement à gauche, porte le nom b1, | ||
| + | # le bit suivant, totalement a gauche dans notre exemple, porte le nom b2.}} | ||
| + | |||
| + | Le lecteur attentif aura noté qu'il y a deux façons de représenter la valeur 3 dans ce système. | ||
| + | |||
| + | * 100 = LED rouge = 3 | ||
| + | * 011 = LED Orange + LED verte = 2+1 = 3 | ||
| + | |||
| + | Cet encodage est équivoque! Il sera d'autant plus gênant et fréquent qu'il y a de bits pour codifier la valeur numérique. | ||
| + | |||
| + | === Le codage binaire === | ||
| + | |||
| + | Plutôt que d'utiliser une série numérique croissante (1,2,3), la codification binaire se propose d' '''utiliser la suite (1,2,4,8,16,32,64,128,...)'''. | ||
| + | |||
| + | Cette suite de valeur est obtenue a partie de 2^0=1, 2^1=2, 2^2=4, 2^3=8 et ainsi de suite. | ||
| + | |||
| + | Ces nouveaux poids pour chacun des bits est visible sur l'image ci-dessous. | ||
| + | |||
| + | [[Fichier:P2E-DIE-intro-11.jpg|360px]] | ||
| + | |||
| + | {{rbox-red| Peut-être l'aurez vous remarqué mais un nombre binaire se lit en commençant par le poids le plus faible.<br />La '''lecture se fait de droite à gauche'''. }} | ||
| + | |||
| + | Cette fois, l'encodage évitera la redondance d'encodage pour la valeur 3 et permettra d'encoder une valeur allant jusque 7. | ||
| + | |||
| + | {| class="wikitable" border="1" | ||
| + | |- | ||
| + | | align="center" | Valeur binaire | ||
| + | | align="center" | LEDs correspondantes | ||
| + | | align="center" | Valeur numérique | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | 000 | ||
| + | | align="left" | toutes LEDs éteintes | ||
| + | | align="left" | 0 | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | 001 | ||
| + | | align="left" | LED rouge = 1 | ||
| + | | align="left" | 1 | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | 010 | ||
| + | | align="left" | LED orange = 2 | ||
| + | | align="left" | 2 | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | 011 | ||
| + | | align="left" | LED orange + LED rouge = 2 + 1 | ||
| + | | align="left" | 3 | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | 100 | ||
| + | | align="left" | LED verte = 4 | ||
| + | | align="left" | 4 | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | 101 | ||
| + | | align="left" | LED verte + LED rouge = 4 + 1 | ||
| + | | align="left" | 5 | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | 110 | ||
| + | | align="left" | LED Verte + LED orange = 4 + 2 | ||
| + | | align="left" | 6 | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | 111 | ||
| + | | align="left" | LED Verte + LED orange + LED rouge = 4 + 2 + 1 | ||
| + | | align="left" | 7 | ||
| + | |} | ||
| + | |||
| + | A bit équivalent, l'encodage binaire permet d'encoder une gamme plus large de valeurs numériques. | ||
| + | |||
| + | Ainsi, sur 4 bits il est possible d'encoder 16 valeurs (0 à 15) en binaire là où l'encodage simple est limité à 11 valeurs (0 à 10). | ||
| + | |||
| + | Sur 5 bits, l'encodage binaire monte à 32 valeurs encodées là où l'encodage simple est limité à 16 valeurs. | ||
| + | |||
| + | Voici un petit résumé graphique du calcul sur base de la valeur binaire 01000110 (que l'on note 0b01000110 en Python) | ||
| + | |||
| + | [[Fichier:P2E-DIE-intro-12.png|480px]] | ||
| + | |||
| + | A titre d'information, sur 8 bits, il est possible d'encoder les valeurs de 0 à 255 et sur 16 bits il sera possible de coder les nombres de 0 à 65535 (Le nombre de bits étant virtuellement illimités sous Python). | ||
| + | |||
| + | === Et sous Python? === | ||
| + | |||
| + | Jusqu'à maintenant, la notation binaire était assez spartiate avec seulement des 1 et des 0. | ||
| + | |||
| + | Cependant, dans un langage de programmation il est important d'indiquer si nous sommes face à une valeur binaire ou une valeur numérique. | ||
| + | |||
| + | Par défaut, Python considère un nombre comme étant encodé en base 10. | ||
| + | |||
| + | {{dbox-gray| Pour signaler un nombre binaire, celui-ci est précédé du préfixe "0b" (ex: 0b110).}} | ||
| + | |||
| + | En saisissant l'instruction si dessous, il est possible de connaître la valeur correspondante d'un nombre binaire | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | print( 0b110 ) | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Ce qui affichera la valeur 6 dans la session REPL comme le démontre la capture Thonny IDE ci-dessous. | ||
| + | |||
| + | [[Fichier:P2E-DIE-20.png]] | ||
| + | |||
| + | Il est également possible de transformer une valeur numérique en sa représentation binaire à l'aide de la fonction {{fname|bin()}} | ||
| + | |||
| + | <syntaxhighlight lang="python"> | ||
| + | print( bin(3) ) | ||
| + | print( bin(6) ) | ||
| + | </syntaxhighlight> | ||
| + | |||
| + | Comme le montre la capture d'écran ci-dessous, {{fname|bin()}} retourne une chaîne de caractère et '''n'utilise que le nombre de bits nécessaires''' pour encoder la valeur numérique. | ||
| + | |||
| + | C'est ainsi que seul 2 bits sont nécessaire pour l'encodage binaire de 3 là où il faut 3 bits pour encoder les valeurs de 4 à 7 (donc aussi pour 6). | ||
| + | |||
| + | [[Fichier:P2E-DIE-21.png]] | ||
== Brancher == | == Brancher == | ||
| − | + | {| class="wikitable" border="1" | |
| + | |- | ||
| + | | align="center" | '''Pico''' | ||
| + | | align="center" | '''Pico-2-Explorer''' | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | GP10 | ||
| + | | align="left" | Btn 1 | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | GP22 | ||
| + | | align="left" | LED verte (bit 0, poids faible) | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | GP26 | ||
| + | | align="left" | LED orange (bit 1) | ||
| + | |- style="font-size: 90%" | ||
| + | | align="left" | GP27 | ||
| + | | align="left" | LED rouge (bit 2, poids fort) | ||
| + | |} | ||
| + | |||
| + | Appuyer sur le bouton générera un nouveau nombre aléatoire qui sera affiché: | ||
| + | # En base 10 dans la session REPL. | ||
| + | # En binaire (base 2) sur les LEDs. | ||
| + | |||
| + | [[Fichier:P2E-DIE-wiring-00.jpg|800px]] | ||
| + | |||
| + | A cause de la disposition des LEDs, le '''décodage du nombre binaire''' ne se fait pas de gauche à droite (comme présenté dans l'introduction) mais '''de bas en haut'''. | ||
| + | |||
| + | Il est commun d'avoir les nombres les plus faible en bas... le poids le plus faible (valeur 1) se trouve donc en bas. | ||
| + | Il est possible de retrouver une lecture normale en faisant pivoter le Pico-2-Explorer de 90° dans le sens anti-horlogique. | ||
== Code == | == Code == | ||
| Ligne 18 : | Ligne 192 : | ||
<syntaxhighlight lang="python" line> | <syntaxhighlight lang="python" line> | ||
| + | import micropython, time | ||
| + | from random import randint | ||
| + | from machine import Pin | ||
| + | micropython.alloc_emergency_exception_buf(100) | ||
| + | |||
| + | counter = 0 | ||
| + | |||
| + | def bouton_cb( obj ): | ||
| + | global counter | ||
| + | counter += 1 | ||
| + | |||
| + | btn = Pin( Pin.board.GP10, Pin.IN, Pin.PULL_UP ) | ||
| + | btn.irq( handler=bouton_cb, trigger=Pin.IRQ_FALLING ) | ||
| + | LEDs = [ Pin(Pin.board.GP27, Pin.OUT), Pin(Pin.board.GP26, Pin.OUT), | ||
| + | Pin(Pin.board.GP22, Pin.OUT) ] | ||
| + | for led in LEDs: | ||
| + | led.value(0) | ||
| − | + | old_value = 0 | |
| + | while True: | ||
| + | if counter>0: # Button pressed? | ||
| + | new_value = randint(1,6) | ||
| + | while new_value == old_value: | ||
| + | new_value = randint(1,6) | ||
| + | |||
| + | old_value = new_value | ||
| + | print( 'Random = %i = %s' % (new_value,bin(new_value)) ) | ||
| + | |||
| + | s = bin(new_value).replace( '0b','' ) | ||
| + | s = '%3s' % s | ||
| + | s = s.replace(' ', '0') | ||
| + | # print( bin(new_value), '->', s ) | ||
| + | |||
| + | for i in range(3): # 0..2 | ||
| + | LEDs[i].value( int(s[i]) ) | ||
| + | |||
| + | time.sleep_ms( 500 ) | ||
| + | # Reset button detection | ||
| + | counter=0 | ||
| + | else: | ||
| + | time.sleep_ms(200) | ||
</syntaxhighlight> | </syntaxhighlight> | ||
| − | La | + | Cette exemple utilise le principe d'interruption pour détecter la pression du bouton. Ce principe est décrit dans [[P2E-MELODIC-BELL|sonnette]]. |
| + | |||
| + | * '''Ligne 2''' : import de la fonction {{fname|randint()}} qui permet de générer un nombre aléatoire entier borné en hait et en bas. | ||
| + | * '''Ligne 4 à 13''' : mise en place de la détection du bouton (voir le projet [[P2E-MELODIC-BELL|sonnette]]). | ||
| + | * '''Ligne 14''' : Déclaration de la liste {{fname|LEDs}} contenant les instances de broches configurées en sortie. La première entrée de la liste {{fname|LEDs[0]}} correspond au bit 2 (poids le plus fort). La deuxième entrée {{fname|LEDs[1]}} correspond au bit 1. La troisième entrées {{fname|LEDs[2]}} correspond au bit 0 (poids le plus faible). Il se fait que c'est aussi dans ce même ordre que {{fname|bin()}} fournit les différents bits. En effet, {{fname|bin(6)}} => "0b110" et si l'on retire le "0b" nous avons une chaîne de caractères "110" où "110"[0] est le bit de poids fort (bit 2) et "110"[2] est le bit de poids faible (bit 0). | ||
| + | * '''Lignes 16 et 17''' : passe toutes les LEDs en revue et place la broche au niveau bas. | ||
| + | * '''Ligne 19''' : déclaration de la variable {{fname|old_value}} contenant la valeur du dé généré au tour précédent. La 0 est placé dans la variable puisqu'il n'y a pas encore de valeur précédente. | ||
| + | * '''Ligne 20''' : boucle infinie sur les lignes 21 à 41 pour détecter: | ||
| + | *# la pression du bouton, | ||
| + | *# généré un nombre aléatoire | ||
| + | *# afficher la valeur sur les LEDs | ||
| + | * '''Lignes 21, 40, 41''' : Détecte '''si''' le bouton est pressé (donc exécution de 22 à 39) '''sinon''' instaurer une pause de 200ms avant la prochaine tentative de détection. | ||
| + | * '''Ligne 22''' : a ce state, le bouton à été pressé. La première opération est de générer un nombre aléatoire entre 1 et 6. | ||
| + | * '''Lignes 23 et 24''' : si la nouvelle valeur {{fname|new_value}} est identique à la précédente alors la boucle {{fname|while}} générera une nouvelle valeur aléatoire. | ||
| + | {{tmbox | text = D'un point de vue aléatoire, il est tout à fait possible de tirer deux fois le chiffre "5" à la suite.<br />Cependant, comme il n'y a pas de lancé de dé, il n'est pas possible de voir qu'un second tirage identique a été effectué. L'utilisateur pourrait croire que la pression du bouton n'a pas été détecté par le programme.<br />Pour éviter cet état de fait, le script génère assurément un nouveau nombre différent du cycle précédent. }} | ||
| + | * '''Ligne 26''' : un nouveau nombre est maintenant disponible, ce dernier est alors stocké dans {{fname|old_value}} pour le prochain tour. | ||
| + | * '''Ligne 27''' : affichage du nombre et sa représentation binaire. | ||
| + | * '''Ligne 29''' : transforme un nombre en sa représentation binaire. Pour rappel, la représentation binaire ne contient que le nombre de bits nécessaires. Par exemple si {{fname|new_value}} contient 3 alors {{fname|bin()}} produira la chaîne de caractères "0b11". La méthode {{fname|replace()}} enlève le préfixe "0b"... il ne reste que les bits. | ||
| + | * '''Lignes 30 et 31''' : Le représentation binaire dont nous avons besoin doit avoir 3 bits. Grâce à une astuce de formatage avec "%3s", la chaîne de caractères va être augmentée, si nécessaire, en 3 positions par insertion d'espace à gauche. Ainsi {{fname|"%3s" % "11"}} produira alors " 11". Pour une valeur de 5, {{fname|"%3s" % "101"}} produira un contenu inchangé (donc "101"). Enfin, la ligne 31 permet de remplacer les espaces (ceux insérés par le formatage) par des "0". Dans l'exemple ci-avant {{fname|" 11".replace(" ","0")}} produira la chaîne de caractères "011". | ||
| + | * '''Lignes 34 et 35''' : la variable {{fname|s}} contient la représentation binaire du nombre aléatoire, par exemple "011" (3). Ainsi s[0] retourne le bit de poids fort (donc "0") tandis que s[2] retourne le bit de poids faible ("1"). Il se fait que la liste {{fname|LEDs}} est organisée dans le même ordre avec {{fname|LEDs[0]}} branché sur la LED indiquant l'état du bit 2 (bit de poids fort). Ainsi {{fname|LEDs[0].value( 1 )}} allume la LED du bit 2. Ainsi, si la valeur 1 est remplacée par la valeur du bit de poids fort, donc {{fname|s[0]}} que l'on converti en entier à l'aide de {{fname|int(s[0])}} permet de modifier l'état de la LED de façon élégante. Pour résumer {{fname|LEDs[0].value( int(s[0]) )}} pour le poids fort, {{fname|LEDs[1].value( int(s[1]) )}} et {{fname|LEDs[2].value( int(s[2]) )}} pour le bit de poids faible. La boucle {{fname|for}} permet d'utiliser un index {{fname|i}} allant de 0 à 2. | ||
| + | * '''Lignes 37 et 39''' : Insertion d'une pause d'une demi-seconde pour laisser le temps de retirer le doigt du bouton (et éviter une seconde activation par rebond) avant de réinitialiser le compteur de détection. | ||
| + | |||
| + | == Ressources == | ||
| + | * [https://docs.micropython.org/en/latest/library/random.html Module random] utilisé pour générer des valeurs aléatoires. | ||
| + | * [https://docs.micropython.org/en/latest/library/machine.Pin.html Machine.Pin] : cette ressource de MicroPython reprend, entre autre, la documentation sur les interruption et les broches. | ||
| + | * [https://docs.micropython.org/en/latest/reference/isr_rules.html Développement avec interruption] : cette ressource de MicroPython reprend de nombreuses recommandations concernant le développement de routines d'interruption avec MicroPython. | ||
{{P2E-TRAILER}} | {{P2E-TRAILER}} | ||
Version actuelle datée du 5 avril 2025 à 14:47
Dé binaire
L'idée dans ce projet est de choisir un nombre au hasard entre 1 et 6 lorsque l'utilisateur presse sur un bouton (pour lancer le dé).
Depuis la plus tendre enfance, nous sommes tous habitué à utiliser la base 10. Ainsi, la lecture d'une valeur numérique quelconque n'est généralement pas un problème... et encore moins pour un dé offrant une valeur entre 1 et 6 en chiffre ou dé utilisant 1 à 6 points.
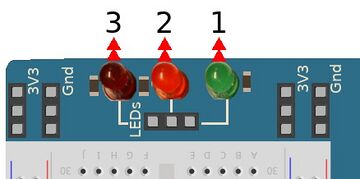
Malheureusement, le Pico-2-Explorer ne dispose pas de LEDs organisées sous la forme de dé ou afficheur numérique. Par contre la carte dispose de 3 LEDs qui peuvent être utilisée pour afficher des 1 (allumée) et des 0 (éteinte).
Il est possible d'utiliser les LEDs du Pico-2-explorer pour représenter une valeur numérique à l'aide d'un encodage binaire.
Nous pourrons ainsi produire une valeur numérique de 1 à 6 (celles d'un dé) qu'il sera possible de lire sur les 3 LEDs du Pico-2-Explorer.
La connaissance des premières représentations binaire peut s'avérer très utile dans les mondes de l'informatique et de l'électronique.
A propos de l'encodage binaire
Plutôt que d'aborder l'encodage binaire de front, je vais procéder par une approche détournée suivit d'une petite correction.
Une approche imparfaite
Admettons que l'on fixe une valeur prédéterminée à nos trois LEDs. Soit les valeurs 1, 2, 3 (en commençant la numérotation par la gauche).
Il est donc possible d'indiquer les valeurs suivantes en allumant la LED appropriée. On peu indiquer quelle LED est allumée à l'aide d'une suite de 1 et de 0. Par exemple 001 indique que seule la LED la plus a droite est allumée tandis que 110 indique que les deux LEDs les plus a gauches sont allumées.
Chacun de ces 1/0 sont des équivalents de marche/arret ou vrai/faux ou True/False. Chacune des positions, appelée bit, n'a que deux valeurs possibles.
- 000 = Aucune LED = 0
- 001 = LED verte = 1
- 010 = LED orange = 2
- 100 = LED rouge = 3
En allant un peu plus loin et en sommant les valeurs correspondantes, il est même possible d'atteindre la valeur 6.
Ainsi:
- 101 = LED rouge + LED verte = 3 + 1 = 4
- 110 = LED rouge + LED orange = 3 + 2 = 5
- 111 = LED rouge + LED orange + LED verte = 3 + 2 + 1 = 6
- Le bit le plus à droite à le poids le plus faible (une valeur de 1).
- Le bit le plus a gauche à le poids le plus fort (une valeur de 3).
Nous pouvons aussi donner des noms aux différents bits:
- Le bit de poids le plus faible (le plus à droite) porte le nom de bit 0 (ou b0),
- Le bit suivant, directement à gauche, porte le nom b1,
- le bit suivant, totalement a gauche dans notre exemple, porte le nom b2.
Le lecteur attentif aura noté qu'il y a deux façons de représenter la valeur 3 dans ce système.
- 100 = LED rouge = 3
- 011 = LED Orange + LED verte = 2+1 = 3
Cet encodage est équivoque! Il sera d'autant plus gênant et fréquent qu'il y a de bits pour codifier la valeur numérique.
Le codage binaire
Plutôt que d'utiliser une série numérique croissante (1,2,3), la codification binaire se propose d' utiliser la suite (1,2,4,8,16,32,64,128,...).
Cette suite de valeur est obtenue a partie de 2^0=1, 2^1=2, 2^2=4, 2^3=8 et ainsi de suite.
Ces nouveaux poids pour chacun des bits est visible sur l'image ci-dessous.
La lecture se fait de droite à gauche.
Cette fois, l'encodage évitera la redondance d'encodage pour la valeur 3 et permettra d'encoder une valeur allant jusque 7.
| Valeur binaire | LEDs correspondantes | Valeur numérique |
| 000 | toutes LEDs éteintes | 0 |
| 001 | LED rouge = 1 | 1 |
| 010 | LED orange = 2 | 2 |
| 011 | LED orange + LED rouge = 2 + 1 | 3 |
| 100 | LED verte = 4 | 4 |
| 101 | LED verte + LED rouge = 4 + 1 | 5 |
| 110 | LED Verte + LED orange = 4 + 2 | 6 |
| 111 | LED Verte + LED orange + LED rouge = 4 + 2 + 1 | 7 |
A bit équivalent, l'encodage binaire permet d'encoder une gamme plus large de valeurs numériques.
Ainsi, sur 4 bits il est possible d'encoder 16 valeurs (0 à 15) en binaire là où l'encodage simple est limité à 11 valeurs (0 à 10).
Sur 5 bits, l'encodage binaire monte à 32 valeurs encodées là où l'encodage simple est limité à 16 valeurs.
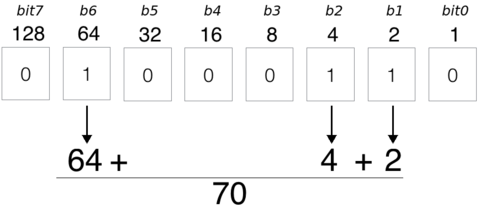
Voici un petit résumé graphique du calcul sur base de la valeur binaire 01000110 (que l'on note 0b01000110 en Python)
A titre d'information, sur 8 bits, il est possible d'encoder les valeurs de 0 à 255 et sur 16 bits il sera possible de coder les nombres de 0 à 65535 (Le nombre de bits étant virtuellement illimités sous Python).
Et sous Python?
Jusqu'à maintenant, la notation binaire était assez spartiate avec seulement des 1 et des 0.
Cependant, dans un langage de programmation il est important d'indiquer si nous sommes face à une valeur binaire ou une valeur numérique.
Par défaut, Python considère un nombre comme étant encodé en base 10.
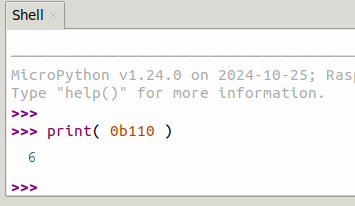
En saisissant l'instruction si dessous, il est possible de connaître la valeur correspondante d'un nombre binaire
print( 0b110 )
Ce qui affichera la valeur 6 dans la session REPL comme le démontre la capture Thonny IDE ci-dessous.
Il est également possible de transformer une valeur numérique en sa représentation binaire à l'aide de la fonction bin()
print( bin(3) )
print( bin(6) )
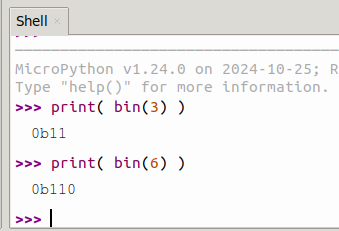
Comme le montre la capture d'écran ci-dessous, bin() retourne une chaîne de caractère et n'utilise que le nombre de bits nécessaires pour encoder la valeur numérique.
C'est ainsi que seul 2 bits sont nécessaire pour l'encodage binaire de 3 là où il faut 3 bits pour encoder les valeurs de 4 à 7 (donc aussi pour 6).
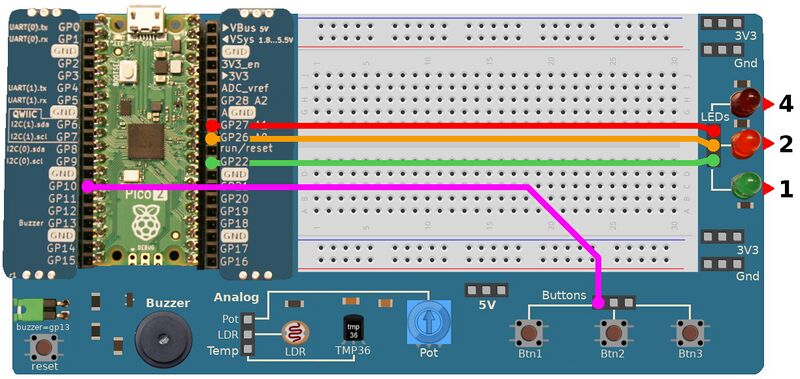
Brancher
| Pico | Pico-2-Explorer |
| GP10 | Btn 1 |
| GP22 | LED verte (bit 0, poids faible) |
| GP26 | LED orange (bit 1) |
| GP27 | LED rouge (bit 2, poids fort) |
Appuyer sur le bouton générera un nouveau nombre aléatoire qui sera affiché:
- En base 10 dans la session REPL.
- En binaire (base 2) sur les LEDs.
A cause de la disposition des LEDs, le décodage du nombre binaire ne se fait pas de gauche à droite (comme présenté dans l'introduction) mais de bas en haut.
Il est commun d'avoir les nombres les plus faible en bas... le poids le plus faible (valeur 1) se trouve donc en bas.
Il est possible de retrouver une lecture normale en faisant pivoter le Pico-2-Explorer de 90° dans le sens anti-horlogique.
Code
Le script die.py est disponible dans le dépôt dédié au Pico-2-Explorer.
1 import micropython, time
2 from random import randint
3 from machine import Pin
4 micropython.alloc_emergency_exception_buf(100)
5
6 counter = 0
7
8 def bouton_cb( obj ):
9 global counter
10 counter += 1
11
12 btn = Pin( Pin.board.GP10, Pin.IN, Pin.PULL_UP )
13 btn.irq( handler=bouton_cb, trigger=Pin.IRQ_FALLING )
14 LEDs = [ Pin(Pin.board.GP27, Pin.OUT), Pin(Pin.board.GP26, Pin.OUT),
15 Pin(Pin.board.GP22, Pin.OUT) ]
16 for led in LEDs:
17 led.value(0)
18
19 old_value = 0
20 while True:
21 if counter>0: # Button pressed?
22 new_value = randint(1,6)
23 while new_value == old_value:
24 new_value = randint(1,6)
25
26 old_value = new_value
27 print( 'Random = %i = %s' % (new_value,bin(new_value)) )
28
29 s = bin(new_value).replace( '0b','' )
30 s = '%3s' % s
31 s = s.replace(' ', '0')
32 # print( bin(new_value), '->', s )
33
34 for i in range(3): # 0..2
35 LEDs[i].value( int(s[i]) )
36
37 time.sleep_ms( 500 )
38 # Reset button detection
39 counter=0
40 else:
41 time.sleep_ms(200)
Cette exemple utilise le principe d'interruption pour détecter la pression du bouton. Ce principe est décrit dans sonnette.
- Ligne 2 : import de la fonction randint() qui permet de générer un nombre aléatoire entier borné en hait et en bas.
- Ligne 4 à 13 : mise en place de la détection du bouton (voir le projet sonnette).
- Ligne 14 : Déclaration de la liste LEDs contenant les instances de broches configurées en sortie. La première entrée de la liste LEDs[0] correspond au bit 2 (poids le plus fort). La deuxième entrée LEDs[1] correspond au bit 1. La troisième entrées LEDs[2] correspond au bit 0 (poids le plus faible). Il se fait que c'est aussi dans ce même ordre que bin() fournit les différents bits. En effet, bin(6) => "0b110" et si l'on retire le "0b" nous avons une chaîne de caractères "110" où "110"[0] est le bit de poids fort (bit 2) et "110"[2] est le bit de poids faible (bit 0).
- Lignes 16 et 17 : passe toutes les LEDs en revue et place la broche au niveau bas.
- Ligne 19 : déclaration de la variable old_value contenant la valeur du dé généré au tour précédent. La 0 est placé dans la variable puisqu'il n'y a pas encore de valeur précédente.
- Ligne 20 : boucle infinie sur les lignes 21 à 41 pour détecter:
- la pression du bouton,
- généré un nombre aléatoire
- afficher la valeur sur les LEDs
- Lignes 21, 40, 41 : Détecte si le bouton est pressé (donc exécution de 22 à 39) sinon instaurer une pause de 200ms avant la prochaine tentative de détection.
- Ligne 22 : a ce state, le bouton à été pressé. La première opération est de générer un nombre aléatoire entre 1 et 6.
- Lignes 23 et 24 : si la nouvelle valeur new_value est identique à la précédente alors la boucle while générera une nouvelle valeur aléatoire.
|
|
D'un point de vue aléatoire, il est tout à fait possible de tirer deux fois le chiffre "5" à la suite. Cependant, comme il n'y a pas de lancé de dé, il n'est pas possible de voir qu'un second tirage identique a été effectué. L'utilisateur pourrait croire que la pression du bouton n'a pas été détecté par le programme. Pour éviter cet état de fait, le script génère assurément un nouveau nombre différent du cycle précédent. |
- Ligne 26 : un nouveau nombre est maintenant disponible, ce dernier est alors stocké dans old_value pour le prochain tour.
- Ligne 27 : affichage du nombre et sa représentation binaire.
- Ligne 29 : transforme un nombre en sa représentation binaire. Pour rappel, la représentation binaire ne contient que le nombre de bits nécessaires. Par exemple si new_value contient 3 alors bin() produira la chaîne de caractères "0b11". La méthode replace() enlève le préfixe "0b"... il ne reste que les bits.
- Lignes 30 et 31 : Le représentation binaire dont nous avons besoin doit avoir 3 bits. Grâce à une astuce de formatage avec "%3s", la chaîne de caractères va être augmentée, si nécessaire, en 3 positions par insertion d'espace à gauche. Ainsi "%3s" % "11" produira alors " 11". Pour une valeur de 5, "%3s" % "101" produira un contenu inchangé (donc "101"). Enfin, la ligne 31 permet de remplacer les espaces (ceux insérés par le formatage) par des "0". Dans l'exemple ci-avant " 11".replace(" ","0") produira la chaîne de caractères "011".
- Lignes 34 et 35 : la variable s contient la représentation binaire du nombre aléatoire, par exemple "011" (3). Ainsi s[0] retourne le bit de poids fort (donc "0") tandis que s[2] retourne le bit de poids faible ("1"). Il se fait que la liste LEDs est organisée dans le même ordre avec LEDs[0] branché sur la LED indiquant l'état du bit 2 (bit de poids fort). Ainsi LEDs[0].value( 1 ) allume la LED du bit 2. Ainsi, si la valeur 1 est remplacée par la valeur du bit de poids fort, donc s[0] que l'on converti en entier à l'aide de int(s[0]) permet de modifier l'état de la LED de façon élégante. Pour résumer LEDs[0].value( int(s[0]) ) pour le poids fort, LEDs[1].value( int(s[1]) ) et LEDs[2].value( int(s[2]) ) pour le bit de poids faible. La boucle for permet d'utiliser un index i allant de 0 à 2.
- Lignes 37 et 39 : Insertion d'une pause d'une demi-seconde pour laisser le temps de retirer le doigt du bouton (et éviter une seconde activation par rebond) avant de réinitialiser le compteur de détection.
Ressources
- Module random utilisé pour générer des valeurs aléatoires.
- Machine.Pin : cette ressource de MicroPython reprend, entre autre, la documentation sur les interruption et les broches.
- Développement avec interruption : cette ressource de MicroPython reprend de nombreuses recommandations concernant le développement de routines d'interruption avec MicroPython.
Traduction augmentée réalisée par Meurisse. D pour shop.MCHobby.be - Licence CC-BY-SA.