P2E-THEREMIN

Page(s) en cours de traduction/élaboration. Page(s) under translation/construction

Theremin

L'idée

A propos de la Photo-résistance

Une même surface masquant la photorésistance, il est instinctivement possible de se rendre compte que luminosité captée va croître/décroître avec le carré de la distance (puisque l'ombre se propage dans les deux directions X et Y.

Cette relation au carré de la distance, même si pas encore démontrée, existe aussi pour la puissance sonore (qui diminue avec le carré de la distance).

C'est pour cette raison que les potentiomètres de réglage de volumes n'ont pas de fonction linéaire mais une fonction logarithmique. Cela donne l' impression à l'oreille d'avoir un réglage du volume qui augmente linéairement avec la rotation du potentiomètre.

Linéaire ou pas, quel importance?

Le but du Theremin est de faire varier le son de façon proportionnelle avec la position de la main au dessus de la photorésistance.

Il est donc nécessaire d'avoir une relation linéaire entre la position de la main et la fréquence du son produit.

Savoir si la relation lumière/résistance de la photo-résistance est linéaire ou pas a donc de toute importance!

Si, comme supposé, la relation lumière/résistance est logarithmique cela signifie que la majorité de la variation de résistance (donc de fréquence du son) s'opère a proximité de la photo-résistance. Dans pareil cas, il faudra faire en sorti de reconvertir la réponse logarithmique vers une réponse linéaire.

Mesures sur la photo-résistance

Il est très facile de se faire une idée de la réponse lumière/résistance en utilisant des conditions d'illumination constante et en pratiquant une série de mesure en positionnant la main à une hauteur donnée puis en mesurant la réponse sur le convertisseur ADC.

En utilisant le câblage du Theremin, le petit script read.py (présent dans le projet Theremin) permet d'effectuer les relevés nécessaires "sans main" (la valeur 99999) puis à 30cm, 25cm, 20cm, 15cm, 10cm, 5cm et enfin 1cm simplement en pressant le bouton lorsque la main est positionnée.

Les valeurs obtenues sont encodées sur 10 bits significatifs (donc de 0 à 1023) pour rester au dessus du bruit (voir tutoriel sur l'entrée analogique).

import micropython, time
from machine import Pin, ADC
micropython.alloc_emergency_exception_buf(100)

counter = 0

def bouton_cb( obj ):
    global counter
    counter += 1
    
# https://docs.micropython.org/en/latest/library/machine.Pin.html
# https://docs.micropython.org/en/latest/reference/isr_rules.html
btn = Pin( Pin.board.GP16, Pin.IN, Pin.PULL_UP )
btn.irq( handler=bouton_cb, trigger=Pin.IRQ_FALLING )

a1 = ADC( Pin( Pin.board.GP27 ) )

read_for_cm = [99999,30,25,20,15,10,5,1]

index = 0
print( "read for %i cm" % read_for_cm[index] )
while True:
    if counter>0: # Button pressed?       
        val = 0
        # Acquire analog on 10 bits
        val = 0
        for i in range( 10 ):
            val += (a1.read_u16()>>6)
        # calculer la moyenne
        val = val/10
        
        print( "    %i of 1024" % vald )
        index += 1
        if index>=len( read_for_cm ):
            index = 0
        
        # next value
        print( "read for %i cm" % read_for_cm[index] )
                
        # Reset button detection
        time.sleep_ms( 500 )
        counter=0
    else:
        time.sleep_ms( 200 )

Ce qui permet de faire un relevé comme celui-ci dessous.

read for 99999 cm
    793 of 1024
read for 30 cm
    770 of 1024
read for 25 cm
    758 of 1024
read for 20 cm
    755 of 1024
read for 15 cm
    742 of 1024
read for 10 cm
    708 of 1024
read for 5 cm
    634 of 1024
read for 1 cm
    499 of 1024

A noter également le minima de 500 et maxima de 793.

En reportant les valeurs dans un tableur, il est clairement possible de voir la progression logarithmique avec le plafonnement vers le maxima.

remarque: la distance 99999 est ici remplacée par 50 pour faciliter le rendu du graphique.

Non seulement cela ressemble à une progression logarithmique mais il serait aussi possible de faire coller un logarithme népérien (fonction ln().

La fonction s'exprime, en première approximation, sous la forme:

y = ln(x)*C+D

avec:

• D = valeur à 1cm car x=1 => ln(1)=0 .
• C = (valeur_à_30cm - D) / ln(30) .

Avec les relevés ci-avant, cela donne:

• D = 499
• C = (770-499)/ln(30) = 79.6778221

La fonction d'approximation s'exprimerait donc:

y = ln(x) * 79.6778221 + 499

La graphique ci-dessous reprend la fonction g(x)=ln(x)*79.6778221+499 (en rouge) et la compare avec les données expérimentales (en bleu).

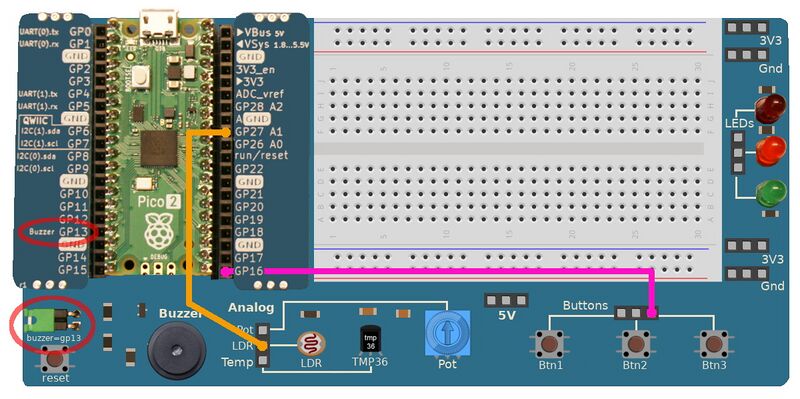
Brancher

Pico	Pico-2-Explorer
GP16	Btn3
GP27	Photo-résistance

xxx

Code

Le script theremin.py est disponible dans le dépôt dédié au Pico-2-Explorer.

1 import micropython, time
2 from random import randint